knight tour algorithm c

• [email protected]

What’s New ?

The Top 10 favtutor Features You Might Have Overlooked

• Don’t have an account Yet? Sign Up

Remember me Forgot your password?

• Already have an Account? Sign In

Lost your password? Please enter your email address. You will receive a link to create a new password.

Back to log-in

By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.

The Knight's Tour Problem (using Backtracking Algorithm)

• Jun 30, 2023
• 6 Minute Read
• Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
• By Vedanti Kshirsagar

Ever wondered how a computer playing as a chess player improves its algorithm to defeat you in the game? In this article, we will learn about the Knight's Tour Problem, the various ways to solve it along with their time and space complexities. So, let's get started!

What is Knight's Tour Problem?

Just for a reminder, the knight is a piece in chess that usually looks like a horse and moves in an L-shaped pattern. This means it will first move two squares in one direction and then one square in a perpendicular direction.

The Knight's Tour problem is about finding a sequence of moves for the knight on a chessboard such that it visits every square on the board exactly one time. It is a type of Hamiltonian path problem in graph theory, where the squares represent the vertices and the knight's moves represent the edges of the graph.

This problem has fascinated many mathematicians for centuries, but the solutions they found were very difficult. The simple solution will be to find every conceivable configuration and selecting the best one is one technique to solve this problem. But that will take a load of time.

One popular solution to solve the Knight's tour problem is Warnsdorff's rule, which involves choosing the next move that leads to a square with the fewest available moves. There is also a backtracking approach. 

 But first moving to all that, let's take a quick understanding of the Hamiltonian path problem.

Hamiltonian Path Problem

The Hamiltonian path problem is a well-known problem in graph theory that asks whether a given graph contains a path that visits every vertex exactly once.

A path that visits every vertex exactly once is called a Hamiltonian path, and a graph that contains a Hamiltonian path is called a Hamiltonian graph. 

Let's take an example of the Hamiltonian path problem. Suppose we have a graph with five vertices and the following edges:

This graph can be represented as:

Knight's Tour Backtracking Algorithm

The backtracking algorithm works by exploring all possible moves for the knight, starting from a given square, and backtracking to try different moves if it reaches a dead end.

Here's the basic outline of the backtracking algorithm to solve the Knight's tour problem:

• Choose a starting square for the knight on the chessboard.
• Mark the starting square as visited.
• For each valid move from the current square, make the move and recursively repeat the process for the new square.
• If all squares on the chessboard have been visited, we have found a solution. Otherwise, undo the last move and try a different move.
• If all moves have been tried from the current square and we have not found a solution, backtrack to the previous square and try a different move from there.
• If we have backtracked to the starting square and tried all possible moves without finding a solution, there is no solution to the problem.

We have given the full C++ program for Backtracking Algorithm to solve Knight's Tour Problem below:

Check the image below before we explain the code:

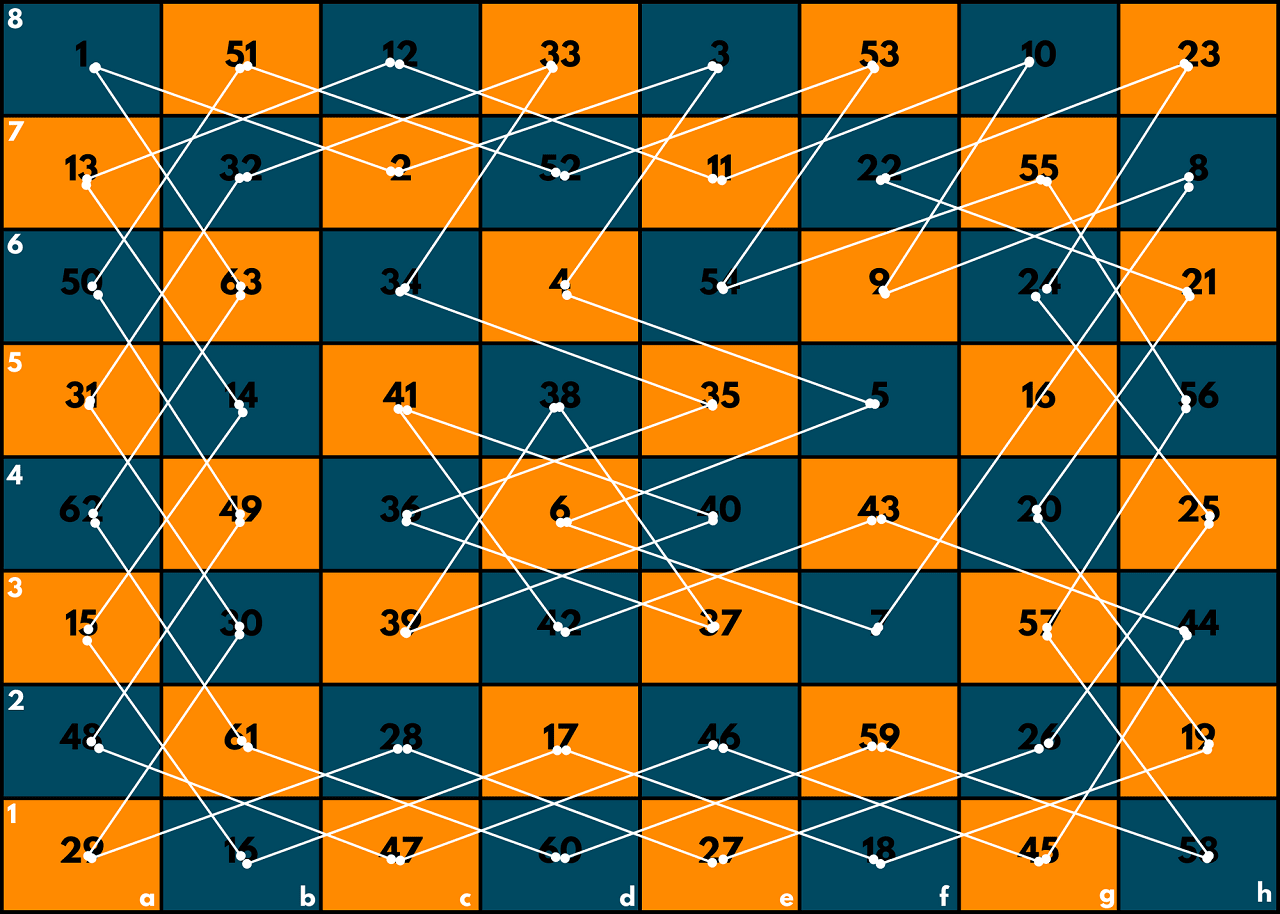
In this implementation, we first define a function validMoves  which takes the current row and column of the knight as input and returns a vector of pairs representing all the valid moves that the knight can make from that position.

The solve function is a recursive function that takes the current row and column of the knight, as well as the current move number, as input. We mark the current square as visited by setting board[row][column] it to the current move number, and then we recursively try all possible moves from the current position.

If we reach the last move, then we found a solution and return true. If no valid move is found from the current position, we backtrack by setting the current square to 0 and returning false.

In the main function, we start the solve function at a specified starting position and then output the number of moves it took to find a solution and print the final chessboard with the solution.

Time & Space Complexity for Backtracking

The backtracking algorithm used to solve the Knight's Tour problem has an exponential time complexity. The number of possible paths for the knight grows very quickly as the size of the chessboard increases, which means that the time taken to explore all possible paths grows exponentially.

The exact time complexity of the Knight's Tour Backtracking algorithm is O(8^(n^2)), where n is the size of the chessboard. This is because each move has a maximum of 8 possible directions, and we have to explore all possible moves until we find a solution.

The space complexity of the backtracking algorithm is O(n^2), where n is the size of the chessboard. So, we can say that the backtracking algorithm is efficient for smaller chessboards.

Warnsdorff's Rule

Warndorff's rule is a heuristic greedy algorithm used to solve this problem. It tries to move the knight to the square with the fewest valid moves, hoping that this will lead to a solution.

Here's an overview of how Warndorff's rule algorithm works:

• Start with a random square on the chessboard.
• From the current square, consider all possible moves and count the number of valid moves from each adjacent square.
• Move to the square with the lowest number of valid moves. In case of a tie, move to the square with the lowest number of valid moves from its adjacent squares.
• Repeat steps 2 and 3 until all squares on the chessboard have been visited.

Here is the pseudocode for Warndorff's rule algorithm:

The time complexity of Warndorff's rule algorithm is O(n^2 log n), where n is the size of the chessboard. This is because we have to visit each square once, and for each square, we have to compute the number of valid moves from each adjacent square. The space complexity of the algorithm is O(n^2) since we need to store the chessboard and the current position of the knight.

Overall, The Knight's Tour problem is related to chess, and solving it can help chess players improve their strategy and become better at the game. In the real world, you can also use it to design efficient algorithms for finding the shortest path between two points in a network.

Now we know The Knight's Tour Problem and its solutions using Backtracking and Warnsdorff's Rule. It has several applications in various fields such as Game theory, Network Routing etc, making it an important problem to study in computer science and mathematics.

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Vedanti Kshirsagar

More by favtutor blogs, monte carlo simulations in r (with examples), aarthi juryala.

The unlist() Function in R (with Examples)

Paired Sample T-Test using R (with Examples)

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Knight's tour problem

What is knight's tour problem.

In the knight's tour problem, we are given with an empty chess board of size NxN, and a knight. In chess, the knight is a piece that looks exactly like a horse. Assume, it can start from any location on the board. Now, our task is to check whether the knight can visit all of the squares on the board or not. When it can visit all of the squares, then print the number of jumps needed to reach that location from the starting point.

There can be two ways in which a knight can finish its tour. In the first way, the knight moves one step and returns back to the starting position forming a loop which is called a closed tour . In the second way i.e. the open tour , it finishes anywhere in the board.

For a person who is not familiar with chess, note that the knight moves in a special manner. It can move either two squares horizontally and one square vertically or two squares vertically and one square horizontally in each direction. So, the complete movement looks like English letter 'L' .

Suppose the size of given chess board is 8 and the knight is at the top-left position on the board. The next possible moves are shown below −

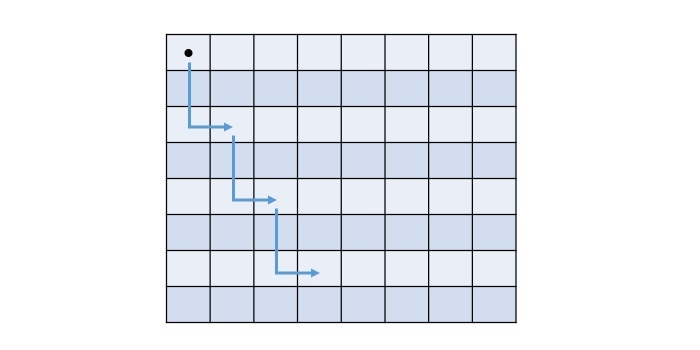
Each cell in the above chess board holds a number, that indicates where to start and in how many moves the knight will reach a cell. The final values of the cell will be represented by the below matrix −

Remember, this problem can have multiple solutions, the above matrix is one possible solution.

One way to solve the knight's tour problem is by generating all the tours one by one and then checking if they satisfy the specified constraint or not. However, it is time consuming and not an efficient way.

Backtracking Approach to Solve Knight's tour problem

The other way to solve this problem is to use backtracking. It is a technique that tries different possibilities until a solution is found or all options are tried. It involves choosing a move, making it, and then recursively trying to solve the rest of the problem. If the current move leads to a dead end, we backtrack and undo the move, then try another one.

To solve the knight's tour problem using the backtracking approach, follow the steps given below −

Start from any cell on the board and mark it as visited by the knight.

Move the knight to a valid unvisited cell and mark it visited. From any cell, a knight can take a maximum of 8 moves.

If the current cell is not valid or not taking to the solution, then backtrack and try other possible moves that may lead to a solution.

Repeat this process until the moves of knight are equal to 8 x 8 = 64.

In the following example, we will practically demonstrate how to solve the knight's tour problem.

Search anything:

Knight’s Tour Problem

Algorithms backtracking.

Open-Source Internship opportunity by OpenGenus for programmers. Apply now.

The Knight's Tour Problem is one of the famous problem in which we have the knight on a chessboard. The knight is supposed to visit every square exactly once.

Following it we have two cases:

• Closed Tour : The knight ends on a square that is one move away from the beginning square. This means that if it continues to move, with the same path that it has followed till now, it will be able to traverse all squares again.
• Open Tour : The knight ends on any other square. This problem is solved on a n x n chessboard. "n" could have any value. This problem is derived from the Hamiltonian Path Problem in Graph Theory .

Hamiltonian Path Problem is focused on finding out if there is a path or route in undirected graph from the beginning to ending node. However, it can gain a lot of complexity even on little increase in its size. Hamiltonian Path is the one that visits each vertex of the graph only once. A grap h with Hamiltonian Path in it is called traceable graph.

However, there are ways to solve this problem in linear time. Consider the below image, let the diamond represent the "knight" and the tick marks represent its possible moves at given position. A "knight" can move two squares in cardinal direction then one square in orthogonal direction.

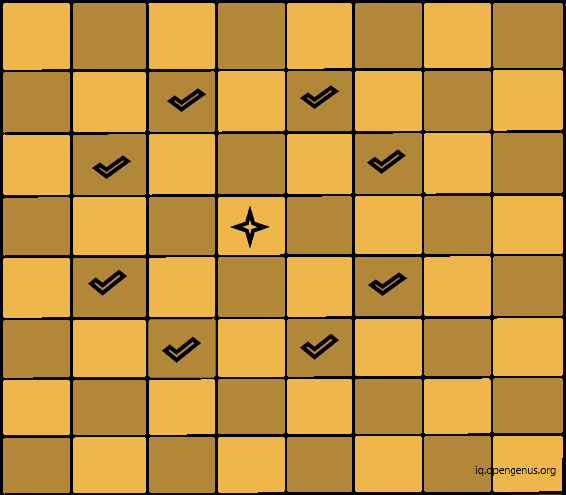
There are many variants possible for this problem like having two knights and so on. In this article we will explore the basic problem with one knight and how it can cover all squares without revisiting them.

One way to solve this problem is Naive Approach, to find all possible configurations and choose the correct one. Since, this would take much longer if the value of n in n x n board is large.

Backtracking

Other technique that can be used for this problem is Backtracking . It is optimized version of our naive technique. Backtracking is the technique in which we try all possible solutions or combinations till we find the one that is correct. In this each combination is tried only once.

It incrementally makes the solution using recursion. We consider on step at a time. If they do not satisfy the constraints then we remove those particular steps.

Time Complexity: O(n * n) for traversing the n x n squares. Implementation:

Explanation:

• The function called in main() would be ans().
• It declares a sol array representing the chess board of n x n size.
• Then we initialise it with -1 values. Then we define the next values of x and y coordinates in array x and array y.
• Now, we call function aux and explore all tours and check if the solution exists.
• If it exists then we print the solution. The aux function:
• This is the recursive function to find the final solution.
• In this we try all possible moves from x and y. We also call function range to check if the squares are in n x n configuration.
• We essentially use backtracking to solve this problem.

We can have much better approaches as well to solve this problem:

Warnsdorff’s algorithm:

In this approach we can start from any initial square on the chess board. Then, we will move to an adjacent, unvisited square with minimum unvisited adjacent squares.

• Set a square as the initial position to start from.
• Mark it with current move number starting with "1".
• Make a set of all positions that can be visited from initial position.
• Mark the square out of the set of possible positions that can be visited with minimum accessibility from initial position as next move number.
• Following the above steps, return the marked board with move numbers with which it has been visited.

In the above code, in find function, we initialized an array of size n x n with values -1.

Then, we initialized x1 and y1 with random values.

Then we copied those values in variables x and y. Now, current positions are same as initial positions.

Then, we mark our first move at location y * n + x.

In the next for loop, we pick next points for our Warnsdorff’s algorithm. We call next function:

• We will try all adjacent squares starting from a random adjacent value with minimum degree.
• We initialize start with a random value
• If now next cell is found then we return false.
• Then, we store coordinates in x and y of next point in variables nx and ny.
• Then, we mark our next move on the array at location ny * n + nx and update next points.

Now, we come back into function find and then neighbor function is called.

• We will check the neighboring squares. If the last square is one move away from the initial location of square then its a closed tour else open tour.

The degree function returns the number of empty squares adjacent to x,y

The range function keeps us within the board and isempty function checks if the square is valid and empty or not.

Now, we again come back to out find function and call print function to print all moves of the knight.

This way,we can implement this algorithm and find our best possible solution.

Neural Networks:

We can even use neural networks to solve this problem. It will be much helpful in the cases where n has much larger value. Each and every possible knight's move is represented by a neuron. Each neuron can have two values : "active" or "inactive". If it is "active" then it is part of our solution else not. This way, we can use machine learning to find solutions to much more complex variants of this problem including large values for "n" and multiple knights.

Using all the above approaches we can find out the best possible solution for our Knight's Tour Problem . Happy Coding!

• Table of Contents
• Course Home
• Assignments
• Peer Instruction (Instructor)
• Peer Instruction (Student)
• Change Course
• Instructor's Page
• Progress Page
• Edit Profile
• Change Password
• Scratch ActiveCode
• Scratch Activecode
• Instructors Guide
• About Runestone
• Report A Problem
• 9.1 Objectives
• 9.2 Vocabulary and Definitions
• 9.3 The Graph Abstract Data Type
• 9.4 An Adjacency Matrix
• 9.5 An Adjacency List
• 9.6 Implementation
• 9.7 The Word Ladder Problem
• 9.8 Building the Word Ladder Graph
• 9.9 Implementing Breadth First Search
• 9.10 Breadth First Search Analysis
• 9.11 The Knight’s Tour Problem
• 9.12 Building the Knight’s Tour Graph
• 9.13 Implementing Knight’s Tour
• 9.14 Knight’s Tour Analysis
• 9.15 General Depth First Search
• 9.16 Depth First Search Analysis
• 9.17 Topological Sorting
• 9.18 Strongly Connected Components
• 9.19 Shortest Path Problems
• 9.20 Dijkstra’s Algorithm
• 9.21 Analysis of Dijkstra’s Algorithm
• 9.22 Prim’s Spanning Tree Algorithm
• 9.23 Summary
• 9.24 Discussion Questions
• 9.25 Programming Exercises
• 9.26 Glossary
• 9.13. Implementing Knight’s Tour" data-toggle="tooltip">
• 9.15. General Depth First Search' data-toggle="tooltip" >

9.14. Knight’s Tour Analysis ¶

There is one last interesting topic regarding the knight’s tour problem, then we will move on to the general version of the depth first search. The topic is performance. In particular, knightTour is very sensitive to the method you use to select the next vertex to visit. For example, on a five-by-five board you can produce a path in about 1.5 seconds on a reasonably fast computer. But what happens if you try an eight-by-eight board? In this case, depending on the speed of your computer, you may have to wait up to a half hour to get the results! The reason for this is that the knight’s tour problem as we have implemented it so far is an exponential algorithm of size \(O(k^N)\) , where N is the number of squares on the chess board, and k is a small constant. Figure 12 can help us visualize why this is so. The root of the tree represents the starting point of the search. From there the algorithm generates and checks each of the possible moves the knight can make. As we have noted before the number of moves possible depends on the position of the knight on the board. In the corners there are only two legal moves, on the squares adjacent to the corners there are three and in the middle of the board there are eight. Figure 13 shows the number of moves possible for each position on a board. At the next level of the tree there are once again between 2 and 8 possible next moves from the position we are currently exploring. The number of possible positions to examine corresponds to the number of nodes in the search tree.

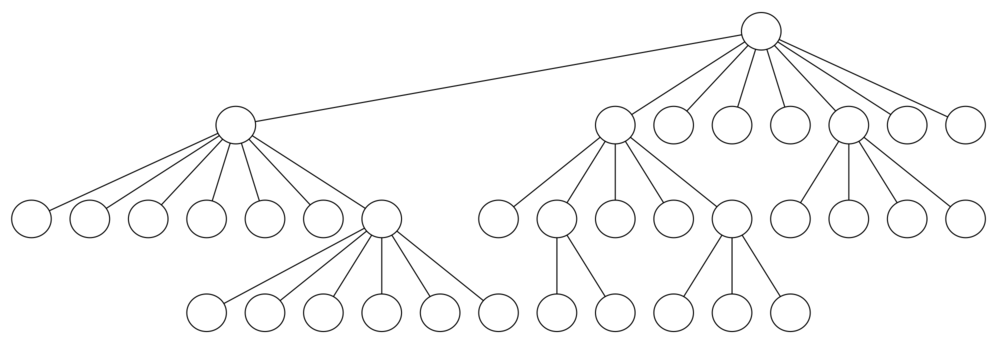
Figure 12: A Search Tree for the Knight’s Tour ¶

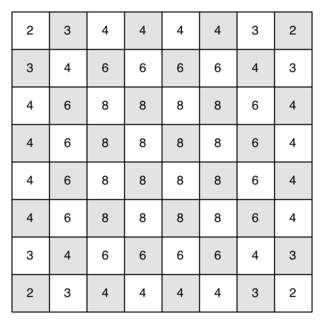
Figure 13: Number of Possible Moves for Each Square ¶

We have already seen that the number of nodes in a binary tree of height N is \(2^{N+1}-1\) . For a tree with nodes that may have up to eight children instead of two the number of nodes is much larger. Because the branching factor of each node is variable, we could estimate the number of nodes using an average branching factor. The important thing to note is that this algorithm is exponential: \(k^{N+1}-1\) , where \(k\) is the average branching factor for the board. Let’s look at how rapidly this grows! For a board that is 5x5 the tree will be 25 levels deep, or N = 24 counting the first level as level 0. The average branching factor is \(k = 3.8\) So the number of nodes in the search tree is \(3.8^{25}-1\) or \(3.12 \times 10^{14}\) . For a 6x6 board, \(k = 4.4\) , there are \(1.5 \times 10^{23}\) nodes, and for a regular 8x8 chess board, \(k = 5.25\) , there are \(1.3 \times 10^{46}\) . Of course, since there are multiple solutions to the problem we won’t have to explore every single node, but the fractional part of the nodes we do have to explore is just a constant multiplier which does not change the exponential nature of the problem. We will leave it as an exercise for you to see if you can express \(k\) as a function of the board size.

Luckily there is a way to speed up the eight-by-eight case so that it runs in under one second. In the listing below we show the code that speeds up the knightTour . This function (see Listing 4 ), called orderbyAvail will be used in place of the call to u.getConnections in the code previously shown above. The critical line in the orderByAvail function is line 10. This line ensures that we select the vertex to go next that has the fewest available moves. You might think this is really counter productive; why not select the node that has the most available moves? You can try that approach easily by running the program yourself and inserting the line resList.reverse() right after the sort.

The problem with using the vertex with the most available moves as your next vertex on the path is that it tends to have the knight visit the middle squares early on in the tour. When this happens it is easy for the knight to get stranded on one side of the board where it cannot reach unvisited squares on the other side of the board. On the other hand, visiting the squares with the fewest available moves first pushes the knight to visit the squares around the edges of the board first. This ensures that the knight will visit the hard-to-reach corners early and can use the middle squares to hop across the board only when necessary. Utilizing this kind of knowledge to speed up an algorithm is called a heuristic. Humans use heuristics every day to help make decisions, heuristic searches are often used in the field of artificial intelligence. This particular heuristic is called Warnsdorff’s algorithm, named after H. C. Warnsdorff who published his idea in 1823.

The visualization below depicts the full process of a Knight’s Tour solution. It portrays the visitation of every spot on the chess board and an analysis on all neighboring locations, and finishes by showing the final solution wherein all locations on the chess board have been visited. The Warnsdorff heuristic is used in this visualization, so all neighbors with less moves are prioritized over neighbors with more moves. The individual components of the visualization are indicated by color and shape, which is described below.

The currently focused point on the chess board is a black circle.

Neighbors of that point that are being examined are higlighted in blue hexagon.

Distant neighbors are orange or brown triangles.

Triangles are orange if the spot on the chess board has not been visited yet.

Triangles are brown if the spot on the chess board has already been visited.

Q-2: What is the big O of the Knight’s Tour function?

• You are correct! K is a small constant, and N is the total number of vertices (or spaces on a chessboard).
• No, the Knight's Tour is not linear.
• No, the Knight's Tour does not have a nested loop that iterates through all values twice.
• No, the input is not processed in a fashion indicative of a factorial.

Knights Tour Algorithm

Explanation

The Knights Tour Algorithm implements backtracking. Given a square “chessboard” (side length denoted by “size”), the algorithm finds a possible solution where a knight can travel to all parts of the board. Each step is printed from 1 to size squared.

Chess videos, game analysis, chess theory and articles. Chess variants, sample games.

“For in the idea of chess and the development of the chess mind we have a picture of the intellectual struggle of mankind.” – Richard Réti

Knight’s Tour: The famous mathematical problem

Chess is a game of strategy and foresight, demanding players to think several moves ahead to outmaneuver their opponents. Among the numerous puzzles and challenges that arise from the complexity of chess, the Knight’s Tour Problem stands out as a particularly fascinating conundrum. The Knight’s Tour is a puzzle that involves moving a knight on a chessboard in such a way that it visits each square exactly once.

The Knight’s Tour Problem is a mathematical challenge that revolves around finding a specific sequence of moves for a knight on a chessboard. It has become a popular problem assigned to computer science students, who are tasked with developing programs to solve it. The variations of the Knight’s Tour Problem go beyond the standard 8×8 chessboard, including different sizes and irregular, non-rectangular boards.

If you’re looking to find your own solution to the Knight’s Tour Problem, there is a straightforward approach known as Warnsdorff’s rule . Warnsdorff’s rule serves as a heuristic for discovering a single knight’s tour. The rule dictates that the knight should always move to the square from which it will have the fewest possible subsequent moves. In this calculation, any moves that would revisit a square already visited are not counted. By adhering to Warnsdorff’s rule, you can systematically guide the knight across the chessboard and ultimately find a knight’s tour.

Modern computers have significantly contributed to the exploration of the Knight’s Tour Problem. Through advanced algorithms and computational power, researchers have been able to tackle larger chessboards and refine existing solutions. However, finding a general solution that works for all chessboard sizes remains elusive.

In conclusion, the Knight’s Tour Problem continues to captivate mathematicians, chess players, and computer scientists alike. Its unique combination of chess strategy, mathematical intricacy, and computational challenges makes it a fascinating puzzle to explore. While the search for a comprehensive solution is ongoing, the journey towards unraveling the mysteries of the Knight’s Tour Problem offers valuable insights into the world of mathematics, algorithms, and the boundless potential of human intellect.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures

Knight’s tour for maximum points

Given a starting position in a 2D matrix representing a grid of points, the task is to find the minimum number of steps required for a knight to collect the maximum points, subject to the following conditions:

• The knight can move only as per the rules of a standard chess knight (i.e. two squares in one direction and one square in a perpendicular direction).
• The knight can collect all the points from all the cells that can be visited in exactly i steps without revisiting any cell.
• If the knight can collect y coins in the x th step, he can fetch all the coins that he will collect in the (x + y) th step, and if the knight can collect z coins in the y th step, he can fetch all the coins that he will collect in the (y + z) th step and so on, without increasing the step count.
• The knight can start and end at any cell on the grid.
• The grid can have any number of rows and columns.

Note: The knight moves exactly the same as the knight on a chess board. Please follow 0-based indexing.

Input: n = 9, m = 10, start_x = 4, start_y = 5 arr = 0 0 0 2 0 2 0 2 0 0 0 0 2 0 2 0 2 0 2 0 0 2 0 0 1 2 0 0 0 2 0 0 2 0 2 0 2 0 2 0 0 2 0 2 0 0 0 2 0 2 0 0 2 0 2 0 2 0 2 0 0 2 0 0 0 2 0 0 0 2 0 0 2 0 2 0 2 0 2 0 0 0 0 2 0 2 0 2 0 0 Output: 1 Explanation: minimum knight have to take 1 steps to gain maximum points. Initially, the knight has 0 coins, he will take 1 step to collect 1 point (sum of cells denoted in red color). Now in the second step, he can collect points from all the cells colored green i.e. 64 points. But with his magical power, at the 1st step, he can fetch points from the (1 + 1)th step. Therefore he can collect 1 + 64 coins at step 1 only. Hence answer is 1. Input: n = 3, m = 3, start_x = 2, start_y = 1 arr = 7 6 8 9 1 4 6 2 8 Output : 0 Explanation: Initially, the knight has 2 points, or more formally we can say that at the 0th step knight has 2 points. In the first step, he can collect points from cells (0, 0) and (0, 2) i.e. 15 points. In the second step, he can collect points from cells (1, 0) and (1, 2) i.e. 13 coins. In the third step, he can collect points from cells (2, 0) and (2, 2) i.e. 14 points. In the fourth step, he can collect points from the cell (0, 1) i.e. 6 points. So in each step, he can collect coins like -You can see in the below image  Knight can collect 15 coins in the 0th step only

Approach: To solve the problem follow the below idea:

The idea is to to explore all the valid neighboring cells from the current cell using BFS traversal, and keep track of the visited cells. Now, calculate the total points collected by the knight, and add the points to a list at each level. After the BFS completes, find the maximum sum of points that can be collected and return the level at which the maximum sum is collected.

Below are the steps for the above approach:

• Create a 2d visited array of size n*m to keep track of visited cells.
• visited[start_x][start_y] = true.
• Create a queue to perform BFS traversal and push the starting position in the queue.
• Create a list to store the sum of points collected at each level of the BFS traversal
• Initialize a variable say size and store the size of the current level by getting the size of the queue.
• Initialize a variable_points = 0 for the current level.
• Run a loop to process all the cells at the current level.
• Dequeue the front element of the queue and store its x and y coordinates.
• Add the points at the current cell to the total points collected, points += arr[x][y] .
• Visit all the neighboring cells that are valid and have not been visited before.
• Store the new x and y coordinates of the neighboring cell using the dx and dy arrays and check if it is valid and has not been visited before, mark it as visited, and add it to the queue .
• Add the sum of points collected at the current level to the list.
• Run a loop from the size of the back side of the point array, list[i] = x , which means we can get x points in the i th step. And do list[i] += list[i + list[i]] .
• Find the max of the list[i] and return the answer.

Below is the code for the above approach:

Time Complexity: O(N*M) Auxiliary Space: O(N*M)

Related Articles:

• Introduction to Matrix or Grid – Data Structure and Algorithms Tutorial

Please Login to comment...

Similar reads, improve your coding skills with practice.

What kind of Experience do you want to share?

Knight's tour algorithm More...

This browser is not able to show SVG: try Firefox, Chrome, Safari, or Opera instead.

Detailed Description

Knight's tour algorithm

A knight's tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path, the tour is closed; otherwise, it is open.

Function Documentation

◆  issafe().

A utility function to check if i,j are valid indexes for N*N chessboard

◆  main()

Main function.

◆  solve()

• backtracking
• knight_tour.cpp

Home Posts Topics Members FAQ

Sign in to post your reply or Sign up for a free account.

Similar topics

By using Bytes.com and it's services, you agree to our Privacy Policy and Terms of Use .

To disable or enable advertisements and analytics tracking please visit the manage ads & tracking page.

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

The Knight's Tour Algorithms in C++

wisn/knights-tour

Folders and files, repository files navigation, knight's tour.

The Knight's tour algorithms in C++. Several algorithms implementation and its outputs included. This repository created for educational purpose.

Implementation

• Brute-force algorithm
• Common backtracking algorithm
• Warnsdorff's rule algorithm

There are several outputs available for each implementation. The solution (output) is based on the Knight's legal moves sequence. Each type of sequence will produces different solution. The default moves is {(1, 2), (2, 1), (-1, 2), (1, -2), (-2, 1), (2, -1), (-2, -1), (-1, -2)} in the form of (x, y) .

As an example, from that sequence above, using the starting point at (0, 0) on the 8x8 chessboard, the output will be:

Then, if we change the sequence to {2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1} in the form of (x, y) , the output will be:

How to generate the outputs?

First, edit the part of n variable which is denoting the chessboard. As an example, edit it to this code below.

Compile the source code into an executable file. I assume that we using the *NIX family operating system and g++ compiler.

Then, using the command line (bash), write this command below.

Edit the {1..100} interval part as we needed. Last, wait until its done.

Brute-force Implementation

There are at least 10 outputs included.

Common Backtracking Implementation

Warnsdorff's rule implementation.

Since the file size is too huge, there are at least 50 outputs included.

Performance Comparison

Since 2x2, 3x3, and 4x4 doesn't have any solution, we skip them.

Hardware Specifications

Tested on the ASUS A455L Notebook with the Intel Core i3-5005U 2GHz and 4GB DDR3 RAM.

Comparison Result

For each algorithm, the form of the result will be A (B, C) where A is the first try success at the random starting point (seconds), B is the number of success starting point(s), and C is the number of fails starting point(s). The fails starting point could be either timeout or no solution found. The timeout limit is 20 seconds for each starting point.

The Warnsdorff's Rule just took about 0.07s for finding a random solution (in the first try) on the 100x100 chessboard.

Margin of Error

Please take a note that the Brute-force and the common backtracking analysis result contains margin of error. The first try result from random starting point is only taken by one arbitrary sample which is not the optimal one. Hence, there may be unfair result occurred.

Source Code License

Licensed under The MIT License . You could use the source code for whatever you want as long as the LICENSE file or the license header in the source code still there.

Documentation License

All reading materials from this repository is licensed under CC BY 4.0 . You could use this repository as your reference as long as you give the attribution.